Molecular Control Volume
The physical laws governing fluid flow, and pretty much everything else in classical physics, are stated as the conservation of mass and energy
together with the requirement that momentum is equal to impressed forces (Newton's Law).
Fluid dynamics, as a branch of continuum mechanics, assumes that we can define these conservation laws at any point in space.
The implicit assumption is the existence of a continuous field at any point in space, so we have a fluid field which can be differentiated.
In Continuum form, these conservation law are expressed by the following equations of fluid dynamics,
for mass conservation,
\begin{align}
\frac{\partial \rho }{\partial t} + \nabla_\beta (\rho u_\beta) = 0. \label{mass}\tag{1}
\end{align}
where \(\rho\) is density and \(u_\beta\) the velocity with greek subscripts index notation (using the
Einstein summation convention).
For Newton's law, the equation becomes,
\begin{align}
\frac{\partial \rho u_\alpha}{\partial t} + \nabla_\beta \left[ \rho u_\alpha u_\beta - \Pi_{\alpha \beta} \right] + F_{\alpha ext} = 0. \label{momentum}\tag{2}
\end{align}
where \(\Pi_{\alpha \beta}\) is a pressure tensor obtained by a reexpression of the impressed force in Newton's law, \(F_s = \nabla_\beta \Pi_{\alpha \beta}\).
Finally, energy conservation is given by,
\begin{align}
\frac{\partial }{\partial t} \rho \mathcal{E} \! = - \nabla_\beta \left[ \rho \mathcal{E} u_\beta + \Pi_{\alpha \beta} u_\alpha + Q_\beta \right], \label{energy}\tag{3}
\end{align}
and \(\mathcal{E}\) is energy.
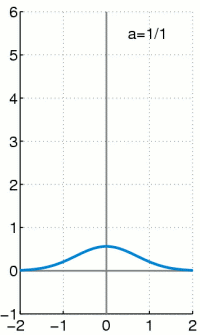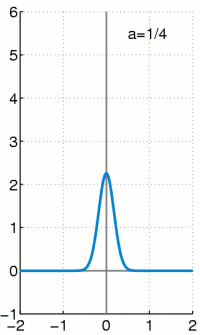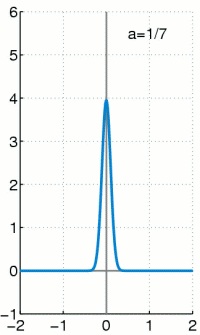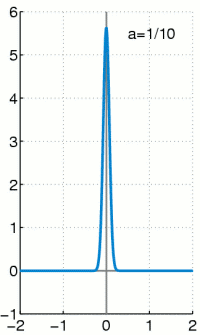 A derivation of these equations can be found in any fluid dynamics textbook and is also covered in my recent lectures online.
These equations are based on a continous field, and the same assumption in a molecular system results in a
Dirac delta functional, an infinitely high, infinitely thin peak.
Conceptually, this infinite limit is identical to the process used in many physicists derivations of field based equations.
An infinitesimal is defined and taken to this same limit.
The Dirac delta functional is therefore a direct consequence of the continuum assumption.
The equivalence between a continuum expression for density and the molecular equivalent can be seen to be,
\begin{align}
\rho(\boldsymbol{r},t) \equiv \displaystyle\sum_{i=1}^{N} m_i \delta(\boldsymbol{r}_i-\boldsymbol{r}). \label{massdensity} \tag{4}
\end{align}
where the delta functional is three dimensional and can be seen to be the product of a function in each direction,
\(\delta(\boldsymbol{r}_i-\boldsymbol{r}) = \delta(x_i-x)\delta(y_i-y)\delta(z_i-z)\).
This is the form given in the seminal work of
A derivation of these equations can be found in any fluid dynamics textbook and is also covered in my recent lectures online.
These equations are based on a continous field, and the same assumption in a molecular system results in a
Dirac delta functional, an infinitely high, infinitely thin peak.
Conceptually, this infinite limit is identical to the process used in many physicists derivations of field based equations.
An infinitesimal is defined and taken to this same limit.
The Dirac delta functional is therefore a direct consequence of the continuum assumption.
The equivalence between a continuum expression for density and the molecular equivalent can be seen to be,
\begin{align}
\rho(\boldsymbol{r},t) \equiv \displaystyle\sum_{i=1}^{N} m_i \delta(\boldsymbol{r}_i-\boldsymbol{r}). \label{massdensity} \tag{4}
\end{align}
where the delta functional is three dimensional and can be seen to be the product of a function in each direction,
\(\delta(\boldsymbol{r}_i-\boldsymbol{r}) = \delta(x_i-x)\delta(y_i-y)\delta(z_i-z)\).
This is the form given in the seminal work of
If we instead express the continuum equations in control volume form, we avoid the need to assume a continous field. The control volume is a fundamental concept in fluid dynamics. It is arguable that the integrated, or weak forms, are more fundametal than the field based continuum limits. For mass, this simply states that the change of a mass inside a volume over time is equal to what flows over the surface, \begin{align} \frac{\partial }{\partial t} \int_V \rho dV = - \oint_S \rho \boldsymbol{u} \cdot d\textbf{S}, \label{mass_int} \tag{5} \end{align} This is simply the integral of Eq. \ref{mass} over a volume in space, and the same process can be applied to the Irving and Kirkwood form of density Eq. \ref{massdensity}, \begin{align} \int_V \rho(\boldsymbol{r},t) dV = \int_V \displaystyle\sum_{i=1}^{N} m_i \delta(\boldsymbol{r}_i-\boldsymbol{r} ) dV \label{IK_mass} \tag{6} \end{align} where mass is constant so the requirement is that we have to evaluate the integral of the Dirac delta functional. This process is shown in 2D in the video (right), resulting in the following term which we call the control volume function, \begin{align} \vartheta_i \equiv \int\limits_{x^-}^{x^+} \int\limits_{y^-}^{y^+} \int\limits_{z^-}^{z^+} \delta(x_i-x)\delta(y_i-y)\delta(z_i-z) dxdydz \; \; \; \; \nonumber \\ \!\!\! =\bigg[\bigg[\bigg[ H(x_i-x)H(y_i-y)H(z_i-z) \bigg]_{x^-}^{x^+} \bigg]_{y^-}^{y^+} \bigg]_{z^-}^{z^+} \nonumber \\ \!\!\! = \left[ H(x^+-x_i) - H(x^- - x_i) \right] \; \, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \nonumber \\ \times \left[ H(y^+ - y_i) \; \! - \, H(y^- - y_i) \right] \; \, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \nonumber \\ \times \left[ H(z^+ - z_i) \, - \, H(z^- - z_i) \right], \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \label{CV_function} \tag{7} \end{align} This is a functional to Select Molecular Inside The Heavisides, so it is zero when a molecular is outside the volume and one when the molecule is inside. The result in a molecules simulation can be visualised by highlighting in red only molecules for which this function is non-zero, see cube video on the left below. The real potential of this functional which Select Molecular Inside The Heavisides, comes when we evaluate spatial derivatives as in the process of deriving the continuum field equations. In the \( x \) direction the CV function for molecule \(i\) is, \begin{align} \frac{\partial \vartheta_i}{\partial x} = -\frac{\partial \vartheta_i}{\partial x_i} = \left[ \delta(x^+ - x_i)-\delta(x^- - x_i) \right] S_{xi}, \label{difftheta} \tag{8} \end{align} where the notation \(S_{xi}\) is introduced to be, \begin{align} S_{xi} \equiv \left[ H(y^+ - y_i) \; \! - \, H(y^- - y_i) \right] \; \, \nonumber \\ \left[ H(z^+ - z_i) \, - \, H(z^- - z_i) \right]. \label{Six} \end{align} and Eq. \ref{difftheta} isolates molecules on a 2D rectangular patch in the y z plane. This function has the property of being only non-zero when molecule \(i\) is crossing the surfaces, as shown in video on the right below,